티스토리 뷰
C++ 로 조합을 구현하는 방법을 알려주겠다.
nCr = n-1Cr-1 + n-1Cr 라는 식을 이용하여 O(nr) 만에 구하는 방법도 있지만, n,r 이 10만정도 된다면 메모리도 시간도 펑펑 터질 것이다.
그래서 이번 글에는 조합을 빨리 구하는 방법을 알려주겠다. (와아앙아앙아아 짝짝짝짝)
순서는 STL내장함수인 next_permutation 을 사용해서 출력하면된다. (이 글은 나중에 추가될 예정이다)
조합을 구할려면 일단 식을 보자

조합 식
이제 이 식을 직접 구하면 되는데 n! 을 구하고 r! 을 구하려고 하면 mod 값에 나눠버리는 경우가 있어서 매우 까다롭다.
예를 들어보자. mod = 7, 구하려고 하는 수는 5C3 이다.
그러면 5! 을 구하고 3! 을 구하고 2! 을 구하고 5! 구한것에서 3! 을 나누고 2! 을 나누고 mod로 나눈 나머지를 구한다.
이런 경우에는 지금은 숫자가 작아서 괜찮지만 n이 20을 넘어간다면 오버 플로우가 날 것이다.
이번에는 5! % 7 을 구하고 3! % 7 을 구하고 2! % 7 을 구한다음 나눠준다.
이런 경우에는 5! % 7 = 1, 3! % 7 = 6, 2! % 7 = 2 -> 1/(6*2) 는 우리가 구하려는 답이 아니므로 이 역시 답이 아니다.
그래서 factorial 을 구하고 모듈러 인버스의 값을 찾아야 한다.
이 모듈러 인버스의 값을 찾아야 하는데 mod가 소수라면 페르마 소정리가 쓰일 수 있다.
만약 mod가 소수가 아니라면 이 글을 읽어봐라. (추가 예정)
a가 mod M의 역원은
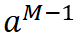
이다.
그래서 a^-1 가 mod M의 역원은

가 된다. 그래서 a^(M-2) 를 O(logM) 만에 구하면 된다. (O(logM) 만에 구하는 법을 모른다면 이 글 을 참고해라.)
이제 준비는 다했다. 답을 식으로 나타내 본다면 n!*pow(r,mod-2)*pow(n-r,mod-2)%mod 가 된다.
이 식을 구하면 전처리 O(N), 쿼리당 O(log mod) 만에 할수 있다.
그리고 factorial inverse 는 factInv[n] = factInv[n+1]*(n+1)%mod 로 전처리가 가능하다.
이런 전처리를 해주면 전처리 O(N), 쿼리당 O(1) 만에 구할 수 있다.
코드를 보자
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll fact[3000005],factInv[3000005],mod = 1e9+7;
ll mpow(ll x,ll m) {
if(!m) return 1;
ll tmp = mpow(x,m/2);
tmp = tmp*tmp % mod;
if(m % 2) return tmp*x%mod;
return tmp;
}
ll Com(ll x,ll r) {
return fact[x]*factInv[r]%mod*factInv[x-r]%mod;
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
fact[0] = 1;
for(int i = 1;i <= 3000000;i++) fact[i] = fact[i-1]*i%mod;
factInv[3000000] = mpow(fact[3000000],mod-2);
for(int i = 2999999;i >= 0;i--) factInv[i] = factInv[i+1]*(i+1)%mod;
int n,r;
cin >> n >> r;
cout << Com(n,r);
}이렇게 nCr 을빠르게 구하는 방법에 대해 알아봤다.
- Total
- Today
- Yesterday
- 냄새 싫어
- DP
- Offline Dynamic Connectivity
- 김춘배
- PS
- 누적 합
- 알고리즘 문제 풀이
- 쿼리
- 정렬
- 스택
- Constructive
- AtCoder
- 비요뜨
- 간단한 풀이
- 1909
- codeforces
- BOJ
- 비요뜨 존맛
- gunwookim
- hyper
- Rabin-Karp
- ABC
- 하이퍼
- 수열과 쿼리
- 앳코더
- 세그먼트 트리
- combination
- 오일러 경로
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
