티스토리 뷰

대학에 진학하고 나서 처음으로 SCPC를 쳤다.
예선 1차는 딱히 쓸게 없어 보여서 쓰진 않았고, 2차도 간단하게 쓸거 같다.
수식 같은거 잘 못쓰고 풀이를 진짜 진짜 못써서 못 알아들을 수도 있다는거 양해 부탁드립니다 ㅠㅠ
문제 5. (9:00 ~ 10:20, 0:00 ~ 1:00)
문제가 처음 열리자 마자 5번 문제를 봤다.
그냥 얼마나 어려운지 체크해보기 위해 문제를 확인한거고, 생각보다 어려워서 고민을 좀 했다.
보물이 있는 A정점을 Ao, 없는 A정점을 Ax, 보물이 있는 B정점을 Bo, 없는 정점을 Bx라 하자.
서브테스크 ? (모든 B는 Bo, 모든 A는 Ao)
사실 문제를 잘못 읽어서 여기서부터 시작했다.
여기서 해본 관찰은
1. A-A 는 A가 이긴다.
2. B-B 는 B가 이긴다.
3. B에서 A가 이기는 정점으로 도달할 수 밖에 없으면 A가 이긴다.
4. A에서 B가 이기는 정점으로 도달할 수 밖에 없으면 B가 이긴다.
고민한지 1시간 째 문제를 잘못읽은 것이 확인되어서 그냥 앞에서부터 풀기로 했다.
문제 1. (10:20 ~ 10:31, 1:20 ~ 1:31) AC
연속된 1이 있는 컴포넌트가 최대 1개여야 하기 때문에
생각보다 쉽게 DP임을 떠올릴 수 있다.
d0[n] : n번째 수까지 모두 0으로 만들 때 최소 비용
d1[n][0] : n번째 수까지 0...01...1 로 만들 때 최소 비용
d1[n][1] : n번째 수까지 0...01...10...0 으로 만들 때 최소 비용
d0[n] = d0[n-1] + E*(a[i] == 1)
d1[n][0] = min(d1[n-1][0],d0[n-1]) + S*(a[i] == 0)
d1[n][1] = min(d1[n-1][0],d1[n-1][1]) + E*(a[i] == 1)
수식 잘못 써서 한번 틀렸다 ㅠ
더 좋은 풀이가 있을 거 같은데 생각하기 귀찮아서 그냥 짜고 AC받았다.
O(N)
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define all(v) v.begin(),v.end()
#pragma gcc optimize("O3")
#pragma gcc optimize("Ofast")
#pragma gcc optimize("unroll-loops")
using namespace std;
const int INF = 1e9;
const int TMX = 1 << 18;
const long long llINF = 1e16;
const long long mod = 1e9+7;
const long long hashmod = 1e9+9;
const int MAXN = 100000;
const int MAXM = 1000000;
typedef long long ll;
typedef long double ld;
typedef pair <int,int> pi;
typedef pair <ll,ll> pl;
typedef vector <int> vec;
typedef vector <pi> vecpi;
int n,a[300005];
ll S,E,d0[300005],d1[300005][2];
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int T; cin >> T;
for(int tc = 1;tc <= T;tc++) {
cin >> n >> S >> E;
for(int i = 1;i <= n;i++) cin >> a[i];
d1[0][0] = d1[0][1] = llINF;
for(int i = 1;i <= n;i++) {
d0[i] = d0[i-1]+E*a[i];
d1[i][0] = min(d1[i-1][0],d0[i-1])+S*(a[i]^1);
d1[i][1] = min(d1[i-1][0],d1[i-1][1])+E*a[i];
}
cout << "Case #" << tc << endl;
cout << min({d1[n][0],d1[n][1],d0[n]}) << endl;
}
}
문제 2. (10:31 ~ 10:57, 1:31 ~ 1:57) AC
W_i 번째 로테이션에서 i가 빠지는 것으로 이해할 수 있고,
각 i마다 end[i] = i번째 프로세스가 빠지는 로테이션의 끝 시간 ( 예를 들어 W_1 = 3, W_2~n > 3 이라면 end[1] = n*3 이 된다.) 를 구해주자.
이는 정렬로 쉽게 해결 가능하다.
다음으로 주어진 쿼리와 end[i]를 시간순으로 정렬해서 end[i]에 도달하면 남은 프로세스 개수를 1 빼주고, 쿼리에 도달하면
현재 남아있는 프로세스 중 앞에서 (쿼리의 시간 - 마지막으로 프로세스를 뺀 시간) mod (남은 프로세스 개수) 번째 프로세스가 답이 되는데, 이를 처리하기 위해서 kth-segment를 사용해주면 된다.
O((N+Q)logN)
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define all(v) v.begin(),v.end()
#pragma gcc optimize("O3")
#pragma gcc optimize("Ofast")
#pragma gcc optimize("unroll-loops")
using namespace std;
const int INF = 1e9;
const int TMX = 1 << 18;
const long long llINF = 1e16;
const long long mod = 1e9+7;
const long long hashmod = 1e9+9;
const int MAXN = 100000;
const int MAXM = 1000000;
typedef long long ll;
typedef long double ld;
typedef pair <int,int> pi;
typedef pair <ll,ll> pl;
typedef vector <int> vec;
typedef vector <pi> vecpi;
int n,Q,t[400005];
ll a[100005],en[100005],ans;
vector <pl> v;
void init() {
v.clear();
ans = 0;
}
void ini(int x,int l,int r) {
if(l == r) {t[x] = 1; return;}
int mid = (l + r) >> 1;
ini(x*2,l,mid), ini(x*2+1,mid+1,r);
t[x] = t[x*2]+t[x*2+1];
}
void update(int x,int l,int r,int wi) {
if(wi < l||r < wi) return;
if(l == r) {
t[x] = 0;
return;
}
int mid = (l + r) >> 1;
update(x*2,l,mid,wi), update(x*2+1,mid+1,r,wi);
t[x] = t[x*2]+t[x*2+1];
}
int query(int x,int l,int r,int kth) {
if(l == r) return l;
int mid = (l + r) >> 1;
if(kth <= t[x*2]) return query(x*2,l,mid,kth);
return query(x*2+1,mid+1,r,kth-t[x*2]);
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int T; cin >> T;
for(int tc = 1;tc <= T;tc++) {
cin >> n >> Q;
init();
for(int i = 1;i <= n;i++) {
cin >> a[i];
v.pb({a[i],i});
}
sort(all(v));
ll la = 0,nam = n,lav = 0;
for(auto [cyc,idx] : v) {
lav += nam*(cyc-la);
la = cyc;
en[idx] = lav; nam--;
}
v.clear();
for(int i = 1;i <= n;i++) {
v.pb({en[i],i});
}
for(int i = 1;i <= Q;i++) {
ll x; cin >> x;
v.pb({x,-i});
}
sort(all(v));
ini(1,1,n);
nam = n, lav = 0;
for(auto [x,idx] : v) {
if(idx < 0) {
idx *= -1;
ans += query(1,1,n,(x-lav-1)%nam+1);
}
else {
lav = x; nam--;
update(1,1,n,idx);
}
}
cout << "Case #" << tc << endl;
cout << ans << endl;
}
}
문제 3. (10:57 ~ 11:47, 1:57 ~ 2:47) AC
경찰관 좌표 q에대한 기댓값을 구해보면
n∑i=1dist(q,posi)∗pi
이다.
x좌표와 y좌표를 분리해서 생각해봐도 된다.
그러면 각 q마다 |q_x-x_i| * p_i + |q_y-y_i| * p_i 를 더하는 문제가 되고, 이는 누적합 (혹은 세그먼트 트리) + lower_bound 로 해결이 가능하다.
O(N+QlogN)
p.s. 테케마다 초기화를 제대로 해준 줄 알았는데 아니었다! 로 6틀을 했다.
p.s.2 cin.tie(NULL) 한 이후에 나오는 모든 줄바꿈을 endl하라 했는데 진짜 하니까 TLE가 떴다. 그래서 C로 바꿔서 냈다. C++ 도 테케 마지막 줄에만 endl해도 되지 않나??
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define mp make_pair
#define all(v) v.begin(),v.end()
#pragma gcc optimize("O3")
#pragma gcc optimize("Ofast")
#pragma gcc optimize("unroll-loops")
using namespace std;
const int INF = 1e9;
const int TMX = 1 << 18;
const long long llINF = 1e16;
const long long mod = 1e9+7;
const long long hashmod = 1e9+9;
const int MAXN = 100000;
const int MAXM = 1000000;
typedef long long ll;
typedef long double ld;
typedef pair <int,int> pi;
typedef pair <ll,ll> pl;
typedef vector <int> vec;
typedef vector <pi> vecpi;
int n,Q;
ld ans[100005];
pair<ll,ld> v[100005];
ll vq[100005];
ld sl[100005],sr[100005],spl[100005],spr[100005];
pl q[100005];
struct Po {
ll x,y;
ld p;
}a[100005];
void init() {
for(int i = 1;i <= Q;i++) ans[i] = 0.0;
}
void getAns() {
sort(v+1,v+n+1);
for(int i = 1;i <= n;i++) {
sl[i] = sl[i-1]+(ld)v[i].x*v[i].y;
spl[i] = spl[i-1]+v[i].y;
}
spr[n+1] = sr[n+1] = 0.0;
for(int i = n;i >= 1;i--) {
sr[i] = sr[i+1]+(ld)v[i].x*v[i].y;
spr[i] = spr[i+1]+v[i].y;
}
for(int i = 1;i <= Q;i++) {
int it = upper_bound(v+1,v+n+1,mp(vq[i],(ld)2))-v-1;
ans[i] += spl[it]*(ld)vq[i]-sl[it] + sr[it+1]-spr[it+1]*(ld)vq[i];
}
}
void pushVal(int op) {
for(int i = 1;i <= n;i++) {
v[i] = {(op ? a[i].y : a[i].x),a[i].p};
}
for(int i = 1;i <= Q;i++) {
vq[i] = (op ? q[i].y : q[i].x);
}
getAns();
}
int main() {
//ios_base::sync_with_stdio(false); cin.tie(0);
int T; scanf("%d",&T);
for(int tc = 1;tc <= T;tc++) {
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%lld %lld",&a[i].x, &a[i].y);
for(int i = 1;i <= n;i++) {
scanf("%Lf",&a[i].p);
}
scanf("%d",&Q);
init();
for(int i = 1;i <= Q;i++) scanf("%lld %lld", &q[i].x, &q[i].y);
pushVal(0);
pushVal(1);
printf("Case #%d\n",tc);
for(int i = 1;i <= Q;i++) printf("%.8Lf\n",ans[i]);
fflush(stdout);
}
}점심. (11:47 ~ 12:10, 2:47 ~ 3:10) AC
맛있는 핫도그를 먹었다. 의지가 충만해진다.
문제 4. (12:10 ~ 1:08, 3:10 ~ 4:08) AC
증명은 제대로 못했는데,
주어진 수를 가장 작은 수를 mn, 가장 큰 수를 mx라 하자.
그러면 n/2개는 mn, n/2개는 mx를 가지는 수열의 '집중노노' 값이 최대가 될 것이다. (홀수의 경우에도 둘 중 아무곳에 +1 해주면 만족한다. 이 글은 쉽게 생각하기 위해 n이 짝수만을 가정한다.)
이를 통해 연산 횟수는 최대 2회임을 알 수 있고, 연산 횟수가 1회만에 가능한지만 판별하면 나머지는 쉽게 해결 가능하다.
어떤 구간 (l, r)에 mn의 개수를 증가시키는 연산을 한다고 할 때, a[1~l-1 + r+1~n] 에 있는 mx개수가 n/2, a[1~l-1 + r+1~n] 에 있는 mn개수가 n/2 - (r-l+1) 개, 구간 (l,r)에 적어도 한개의 mn이 존재하면 1회의 연산만으로 '집중노노'의 값을 최대화 할 수 있다. mn과 mx를 반대로 놓고 동일한 연산을 수행해야 한다.
그러면 구간 (l,r)을 어떻게 구해야 하는가?
투 포인터 알고리즘을 사용하여 l을 고정 시킬 때 a[1~l-1 + r+1~n] 에 있는 mx값이 n/2 을 만족하는 가장 큰 r값이 고정되고, 이는 l이 증가함에 따라 r도 증가한다.
투 포인터 대신 lower_bound(이분탐색)을 사용하는 경우도있지만, 시간제한이 테스트케이스 T(1 <= T <= 3508)개에 대한 전체 수행 시간이 0.5초 이하이기 때문에 log가 붙는 순간 제한시간을 초과하여 불가능 할 것 같다.
edge case 0회 (수열의 수가 모두 동일, 처음부터 '집중노노'의 값을 최대화 하는 수열) 을 조심하자.
O(N)
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define all(v) v.begin(),v.end()
#pragma gcc optimize("O3")
#pragma gcc optimize("Ofast")
#pragma gcc optimize("unroll-loops")
using namespace std;
const int INF = 1e9;
const int TMX = 1 << 18;
const long long llINF = 1e16;
const long long mod = 1e9+7;
const long long hashmod = 1e9+9;
const int MAXN = 100000;
const int MAXM = 1000000;
typedef long long ll;
typedef long double ld;
typedef pair <int,int> pi;
typedef pair <ll,ll> pl;
typedef vector <int> vec;
typedef vector <pi> vecpi;
int n,op;
int a[50005];
int s1[50005],s2[50005];
pi isok(int c1,int c2) { // 1개수 c1, 2개수 c2가 되어야 한다. 2를 증가시키는 연산을 할거다.
int l = 0, r = 1;
for(l = 1;l <= n;l++) {
// l~r에 연산을 취할거다.
r = max(r,l+1);
while(r <= n&&s1[l-1]+s1[n]-s1[r] >= c1) r++;
r--;
if(s1[l-1]+s1[n]-s1[r] == c1&&s2[r]-s2[l-1] > 0&&s2[l-1]+s2[n]-s2[r]+r-l+1 == c2) return {l,r};
}
return {0,0};
}
bool getAns() {
pi ret = isok(n/2,n-n/2);
if(ret.x) {
printf("1\n%d %d %d\n",2-op,ret.x,ret.y);
fflush(stdout);
return true;
}
if(n % 2) ret = isok(n-n/2,n/2);
if(ret.x) {
printf("1\n%d %d %d\n",2-op,ret.x,ret.y);
fflush(stdout);
return true;
}
return false;
}
int result = 0;
char ch;
int readInt () {
result = 0;
ch = getchar();
while (true) {
if(ch == '-') break;
if(ch >= '0' && ch <= '9') break;
ch = getchar();
}
result = ch-'0';
while (true) {
ch = getchar();
if (ch < '0'||ch > '9') break;
result = result*10+(ch-'0');
}
return result;
}
int main() {
//ios_base::sync_with_stdio(false); cin.tie(0);
int T; T = readInt();
for(int tc = 1;tc <= T;tc++) {
n = readInt();
int mn = INF,mx = 0;
for(int i = 1;i <= n;i++) a[i] = readInt(), mn = min(mn,a[i]), mx = max(mx,a[i]);
for(int i = 1;i <= n;i++) {
if(a[i] == mn) a[i] = 1;
else if(a[i] == mx) a[i] = 2;
else a[i] = 0;
}
for(int i = 1;i <= n;i++) {
s1[i] = s1[i-1]+(a[i] == 1);
s2[i] = s2[i-1]+(a[i] == 2);
}
printf("Case #%d\n",tc);
if(s1[n] == n||(s1[n] == n/2&&s2[n] == n-n/2)||(s1[n] == n-n/2&&s2[n] == n/2)) {
printf("0\n");
fflush(stdout);
continue;
}
op = 0;
if(getAns()) continue;
op = 1;
for(int i = 1;i <= n;i++) {
if(a[i] == 1) a[i] = 2;
else if(a[i] == 2) a[i] = 1;
s1[i] = s1[i-1]+(a[i] == 1);
s2[i] = s2[i-1]+(a[i] == 2);
}
if(getAns()) continue;
printf("2\n");
int i1,i2;
for(int i = 1;i <= n;i++) {
if(a[i] == 1) i1 = i;
if(a[i] == 2) i2 = i;
}
if(i1 < i2) {
if(i1 <= n/2) {
printf("%d %d %d\n",2-op,i1+1,n);
printf("%d %d %d\n",op+1,1,n/2);
}
else {
printf("%d %d %d\n",op+1,1,i2-1);
printf("%d %d %d\n",2-op,n/2+1,n);
}
}
else {
if(i2 <= n/2) {
printf("%d %d %d\n",op+1,i2+1,n);
printf("%d %d %d\n",2-op,1,n/2);
}
else {
printf("%d %d %d\n",2-op,1,i1-1);
printf("%d %d %d\n",op+1,n/2+1,n);
}
}
fflush(stdout);
}
}
문제 5. (1:08 ~ 2:41, 4:08 ~ 5:41) AC
도달 가능한 같은 사람의 정점을 같은 컴포넌트로 연결하고 넘버링을 하자.
여기서 중요한 c배열을 정의하겠다.
gans[i] : i번 컴포넌트는 어떤 방법을 사용하더라도 A 가 이긴다(1), B가 이긴다 (-1), 아직 모른다(0).
color[i] : i번 컴포넌트의 주인이 B인가? (A이면 0, B 이면 1)
어떤 컴포넌트 i에 대해,
color[i] = A and 컴포넌트 안에 있는 보물이 있는 정점 수 >= 1 and 컴포넌트 크기 >= 2 -> gans[i] = 1
color[i] = B and 컴포넌트에 존재하는 인접한 두 정점 모두 보물이 없다 -> gans[i] = -1
쉽게 그림으로 예를 들면

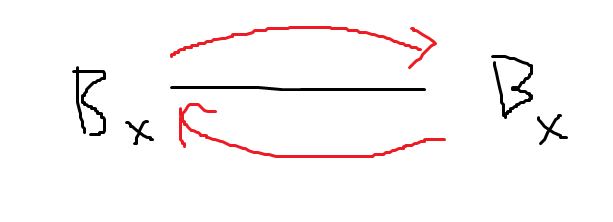
이렇게 된다.
또한 이게 중요한데, 몇가지 관찰을 더 해보면
모두 최적으로 움직인다 가정했을 때
1. 위에서 컴포넌트를 합친것에 의해 A-A, B-B 간선은 없앨 수 있다.
2. Bo -> A 이동은 발생할 수 없다. A가 다시 Bo로 이동시키면 무한히 보물을 얻을 수 있다.
3. Ax -> Bx 이동은 발생할 수없다. Bx가 다시 Ax로 이동시키면 무한히 보물을 얻을 수 없다.
이를 종합해보면
같은 컴포넌트끼리 이동하는 것을 제외했을 때
1. Ax는 무조건 Bo로만 이동해야 한다.
2. Bx는 무조건 Ax로만 이동해야 한다.
3. Ao는 무조건 Bx, Bo로만 이동해야 한다.
4. Bo는 무조건 다른 컴포넌트로 이동할 수 없다.
이것을 그려보면
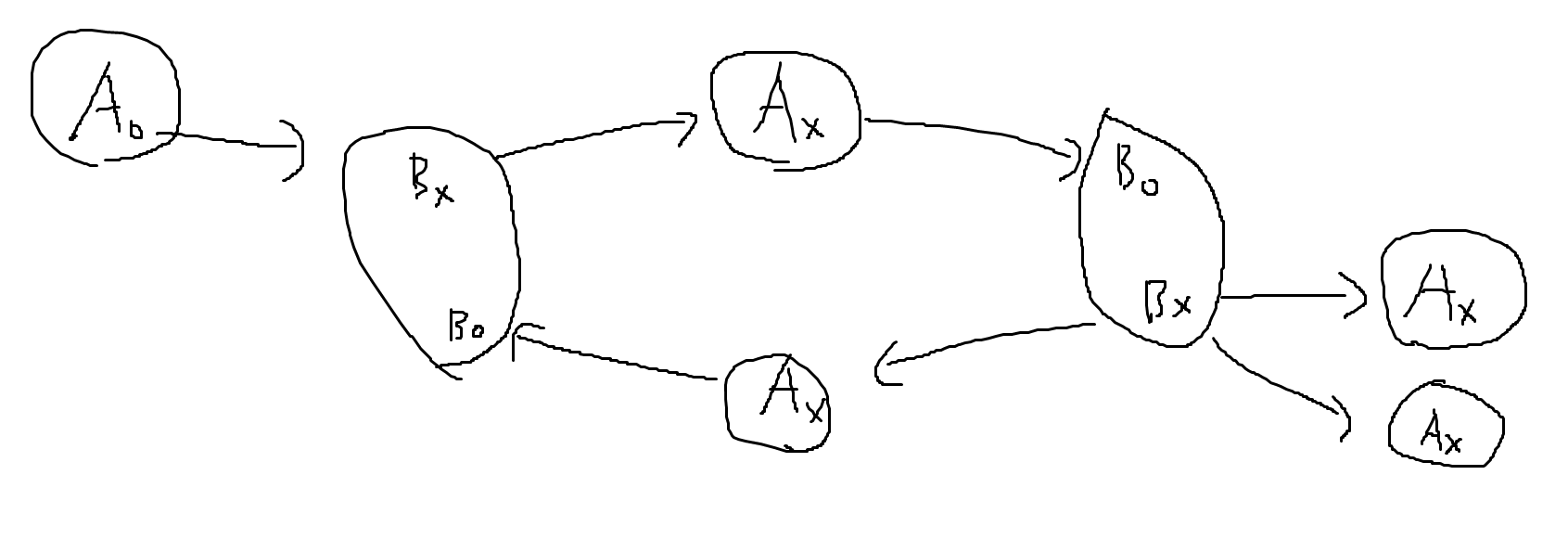
이러한 그래프가 형성 될 것이다.
여기서 위상정렬을 사용하는데
간선의 방향을 뒤집고 위상정렬을 해야 한다.
outdegree[i] = 0 and gans[i] = 0 인 컴포넌트에 대해서 컴포넌트의 주인이 원하는 결과를 얻을 수 없다는 뜻이므로
color[i] = 0 -> gans[i] = -1 (컴포넌트의 주인이 A이고, 이 컴포넌트는 어떤 방법을 써도 보물을 무한히 얻을 수 없다.)
color[i] = 1 -> gans[i] = 1 (주인 B, 보물을 무한히 얻을 수 있다.)
gans[i] != 0인 정점을 다 집어넣고 위상정렬을 하는데
B<-A에서 A가 하나라도 gans = -1이라면 B는 gans = -1 이고
A<-B에서 B가 하나라도 gans = 1이라면 A는 gans = 1 이다.
gans값이 정해진 컴포넌트는 ind !=0 이여도 큐에 추가로 넣을 수 있고, 이를 반복하면 각 컴포넌트마다 'gans값이 정해짐' or '사이클에 의해 gans값이 아직 0임' 이다.
사이클에 의해 gans값이 0이라는 것은 무한히 순환하며 보물을 얻을 수 있다는 말이므로 gans = 1이다.
결국 모든 컴포넌트에 대해 gans값을 구할 수 있고, 답을 출력해낼 수 있다.
O(N+M)
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define all(v) v.begin(),v.end()
#pragma gcc optimize("O3")
#pragma gcc optimize("Ofast")
#pragma gcc optimize("unroll-loops")
using namespace std;
const int INF = 1e9;
const int TMX = 1 << 18;
const long long llINF = 1e16;
const long long mod = 1e9+7;
const long long hashmod = 1e9+9;
const int MAXN = 100000;
const int MAXM = 1000000;
typedef long long ll;
typedef long double ld;
typedef pair <int,int> pi;
typedef pair <ll,ll> pl;
typedef vector <int> vec;
typedef vector <pi> vecpi;
int n,m,gc,A[100005];
int c[100005];
char in[100005];
vec v[100005]; // 정점간 간선
vec vg[100005]; // 컴포넌트 간 간선
vec group[100005]; // i번째 그룹에 어떤 정점이 포함되어 있는지
int co[100005]; // i번 정점이 몇번째 그룹인지
int ist[100005]; // 보물이 있는지
int gco[100005]; // 그룹 색이 뭔지 (0 : A,1 : B)
int gans[100005]; // 무조건 보물을 먹을 수 있는지 (1 : 가능, -1 : 불가능, 0 : 모름)
int ind[100005];
void init() {
gc = 0;
for(int i = 1;i <= n;i++) {
v[i].clear();
vg[i].clear();
group[i].clear();
co[i] = c[i] = gans[i] = 0;
ind[i] = 0;
}
}
void dfs(int x) {
if(co[x]) return;
co[x] = gc;
group[gc].pb(x);
for(int i : v[x]) {
if(A[i] == A[x]) dfs(i);
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
int T; cin >> T;
for(int tc = 1;tc <= T;tc++) {
cin >> n >> m >> in+1;
for(int i = 1;i <= n;i++) A[i] = (in[i] == 'B');
cin >> in+1;
for(int i = 1;i <= n;i++) ist[i] = (in[i] == 'T');
init();
for(int i = 1;i <= m;i++) {
int x,y; cin >> x >> y;
v[x].pb(y), v[y].pb(x);
}
for(int i = 1;i <= n;i++) {
if(co[i]) continue;
gc++; dfs(i);
gco[gc] = A[i];
}
for(int i = 1;i <= gc;i++) {
int cnt = 0;
for(int j : group[i]) cnt += ist[j];
if(!gco[i]&&(cnt&&group[i].size() >= 2)) gans[i] = 1;
if(gco[i]) {
for(int j : group[i]) {
for(int nx : v[j]) {
if(co[j] == co[nx]&&!ist[j]&&!ist[nx]) gans[i] = -1;
}
}
}
}
for(int i = 1;i <= gc;i++) {
for(int j : group[i]) {
for(int nx : v[j]) {
if(A[j]^A[nx]) {
if(!gco[i]) { // A->B
if(ist[j]||ist[nx]) vg[co[nx]].pb(i), ind[i]++;
}
else { // B->A
if(!ist[j]&&!ist[nx]) vg[co[nx]].pb(i), ind[i]++;
}
}
}
}
}
queue <int> q;
for(int i = 1;i <= gc;i++) { // vg를 반대로 넣었음 (업데이트 해야 하기 때문)
if(!ind[i]&&!gans[i]) {
if(!gco[i]) gans[i] = -1;
else gans[i] = 1;
}
if(gans[i]) c[i] = 1, q.push(i);
}
while(!q.empty()) {
int x = q.front(); q.pop();
for(int i : vg[x]) {
ind[i]--;
if(c[i]) continue;
if(!gco[x]&&gans[x] == -1) {
gans[i] = -1;
q.push(i);
c[i] = 1;
continue;
}
if(gco[x]&&gans[x] == 1) {
gans[i] = 1;
q.push(i);
c[i] = 1;
continue;
}
if(!ind[i]) {
if(!gco[i]) gans[i] = -1;
else gans[i] = 1;
q.push(i);
c[i] = 1;
}
}
}
for(int i = 1;i <= gc;i++) {
if(!c[i]) {
gans[i] = 1;
}
}
cout << "Case #" << tc << endl;
for(int i = 1;i <= n;i++) {
cout << (gans[co[i]] == 1 ? 'A' : 'B');
}
cout << endl;
}
}
블로그를 엄청 열심히 쓰려고 하지도 않았고, 누구에게 풀이를 명확히 설명하려고 적은게 아니라 설명이 많이 미흡합니다. 죄송합니다.
- Total
- Today
- Yesterday
- DP
- gunwookim
- 앳코더
- BOJ
- 냄새 싫어
- Constructive
- 누적 합
- 정렬
- 스택
- 세그먼트 트리
- PS
- hyper
- 비요뜨
- 김춘배
- 쿼리
- codeforces
- Offline Dynamic Connectivity
- combination
- 수열과 쿼리
- 오일러 경로
- 간단한 풀이
- 알고리즘 문제 풀이
- ABC
- 하이퍼
- Rabin-Karp
- 비요뜨 존맛
- 1909
- AtCoder
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
